Latin Hypercube Sampling Software Download
DescriptionX = lhsnorm(mu,sigma,n) returnsan n-by- p matrix, X,containing a latin hypercube sample of size n froma p-dimensional multivariate normal distributionwith mean vector, mu, and covariance matrix, sigma.X is similar to a random sample from themultivariate normal distribution, but the marginal distribution ofeach column is adjusted so that its sample marginal distribution isclose to its theoretical normal distribution.X = lhsnorm(mu,sigma,n, flag) controlsthe amount of smoothing in the sample. If flag is 'off',each column has points equally spaced on the probability scale. Inother words, each column is a permutation of the values G(0.5/n),G(1.5/n)., G(1-0.5/n), where G isthe inverse normal cumulative distribution for that column's marginaldistribution. If flag is 'on' (thedefault), each column has points uniformly distributed on the probabilityscale. For example, in place of 0.5/n you use avalue having a uniform distribution on the interval (0/n,1/n).X,Z = lhsnorm(.) alsoreturns Z, the original multivariate normal samplebefore the marginals are adjusted to obtain X.
Apr 25, 2017. USD $100.00, License: Free to try, Author: Express Software Solutions. Nearly Orthogonal Latin Hypercube Sampling. Vose Software specializes in providing software systems for assessing and managing risks using the most precise information possible. Latin Hypercube Sampling Free Download. Monte Carlo sampling technique is used to sample property values within its corresponding uncertainty range i.e. 95%-confidence interval using the software MATLAB (2015b). Latin Hypercube Sampling method can be utilized for probabilistic sampling of the fluid property input space of a compound.
Open Access is an initiative that aims to make scientific research freely available to all. To date our community has made over 100 million downloads. It’s based on principles of collaboration, unobstructed discovery, and, most importantly, scientific progression. As PhD students, we found it difficult to access the research we needed, so we decided to create a new Open Access publisher that levels the playing field for scientists across the world.
By making research easy to access, and puts the academic needs of the researchers before the business interests of publishers. The Monte Carlo method has two disadvantages.
First, it usually needs a very high number of simulations. If the output quantity must be obtained by time-consuming numerical computations, the simulations can last a very long time, and the response surface method is not always usable.

Latin Hypercube Sampling Example
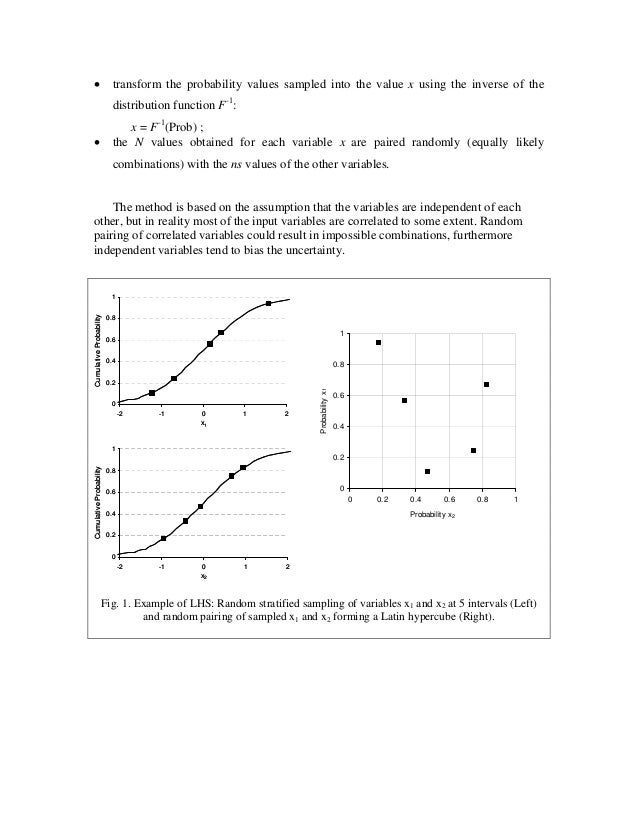
Second, it can happen that the generated random numbers of distribution function F (which serves for the creation of random numbers with nonstandard distributions) are not distributed sufficiently and regularly in the definition interval (0; 1). Sometimes, more numbers are generated in one region than in others, and the generated quantity has thus somewhat different distribution than demanded. This problem can appear especially if the output function depends on many input variables.A method called Latin Hypercube Sampling (LHS) removes this drawback.
The basic idea of LHS is similar to the generation of random numbers via the inverse probabilistic transformation (3) and shown in Chapter 15 ,. The difference is that LHS creates the values of F not by generating random numbers dispersed in chaotic way in the interval (0; 1), but by assigning them certain fix values. The interval (0; 1) is divided into several layers of the same width, and the x values are calculated via the inverse transformation ( F –1) for the F values corresponding to the center of each layer. With reasonably high number of layers (tens or hundreds), the created quantity x will have the proper probability distribution. This approach is called stratified sampling. If the output variable y depends on several input quantities, x 1, x 2., x m, it is necessary that each quantity is assigned values of all layers and that the quantities and layers of individual variables are randomly combined. This is done by random assigning the order numbers of layers to the individual input quantities.

Figure 1.Principle of the LHS method.The procedure is as follows. The definition interval of the distribution function F of each of m variables is divided into N layers.
N, the same for all variables, also corresponds to the number of trials (= simulation experiments). In each trial, the order numbers of layers are assigned randomly to the individual variables ( X 1, X 2., X m).
In this way, various layers of the individual variables are always randomly combined. In practice, this is achieved by means of random numbers and their rank-ordering. Then, each input variable is assigned the value corresponding to the center of the pertinent layer of its distribution function.The application is illustrated on a case with four random quantities ( X 1, X 2, X 3, and X 4) and the definition interval of F divided into five layers. Only five layers are used here for simplicity; usually, several tens of layers are used. In our case, Y will be calculated for five combinations of the four input quantities.
Thus, 5 × 4 = 20 random numbers with uniform distribution in interval (0; 1) are generated (see the table in the left part of ). Then, the layer numbers for variable X 1 (for example) for individual trials are assigned with respect to the order of random values (for X 1) ranked by size from the maximum to minimum. Here, layer no. 3 (with the highest number 0.83) for the first trial, layer no. 1 for the second, no. 5 for the third, no.
2 for the fourth, and no. 4 for the fifth, corresponding to the numbers 0.56 - 0.25 - 0.83 - 0.17 and 0.30 in the column for X 1. Similar operations are done for each variable. Thus, in the first trial, variables X 1, X 2, X 3, and X 4 are assigned the values corresponding to the second, fourth, second, and fifth layers of their distribution functions, respectively. Inverse probabilistic transformation F –1 is then used for the determination X 1 from F 1,1, etc.; see the table on the right. Now, the investigated quantity Y = Y( X 1, X 2, X 3, X 4) is calculated five times.
The obtained values Y 1, Y 2, Y 3, Y 4, and Y 5 can be used for the determination of statistical characteristics (mean, standard deviation.).